一个估阶问题

记 $P(v)=\log\prod\limits_{n\geq 1}\left(\frac 1{1-e^{-nv}}\right)$ ， $f(x)=\log(\frac{xv}{1-e^{-xv}})$ ，则 $f'(x)=\frac1x-\frac{ve^{-xv}}{1-e^{-xv}}$ .

$\int_0^Nf(x)\text dx=Nf(N)-\int_0^Nxf'(x)\text dx=\textcolor{purple}{N\log Nv}+\textcolor{grey}{N\log\frac1{1-e^{-Nv}}}-\textcolor{orange}N+\int_0^N\frac{xv}{e^{xv}-1}\text dx$

一方面由 $\text{String formula}$ 有：

$\sum\limits_{0< x\leq N}f(x)=\underbrace{\log(\prod\limits_{1\leq n\leq N}\frac{1}{1-e^{-nv}})}_{P(N,v)}+N\log v+\log N!\overset{\text{String\ formula}}{=}P(N,v)+\textcolor{purple}{N\log v}+(\textcolor{purple}{N\log N}-\textcolor{orange}{N}+\textcolor{green}{\frac{\log N}{2}}+\frac{\log({2\pi})}{2}+\textcolor{grey}{\frac{\epsilon}{N}})$ ，其中 $\epsilon=\epsilon(N)\in[0,\frac18]$ .

另一方面，由 $\text{Euler-Maclaurin\ formula}$ 有:

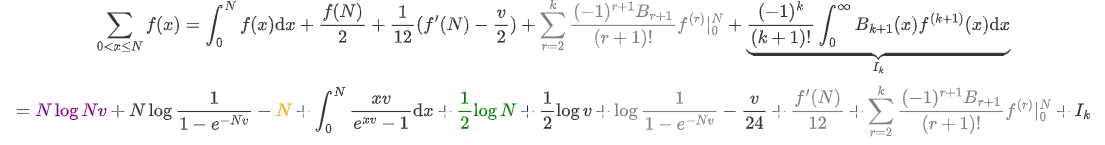
这部分好像显示不了，希望有好心人帮我修一下qwq. $\sum\limits_{0< x\leq N}f(x)=\int_0^Nf(x)\text dx+\frac{f(N)}{2}+\frac{1}{12}(f'(N)-\frac v2)+\textcolor{grey}{\sum\limits_{r=2}^k\frac{(-1)^{r+1}B_{r+1}}{(r+1)!}f^{(r)}|_0^N}+\underbrace{\frac{(-1)^k}{(k+1)!}\int_0^\infty B_{k+1}(x)f^{(k+1)}(x)\text dx}_{I_k}\\=\textcolor{purple}{N\log Nv}+{N\log\frac1{1-e^{-Nv}}}-\textcolor{orange}N+\int_0^N\frac{xv}{e^{xv}-1}\text dx+\textcolor{green}{\frac{1}{2}\log N}+\frac{1}{2}\log v+\textcolor{grey}{\log\frac1{1-e^{-Nv}}}-\frac v{24}+\textcolor{grey}{\frac{f'(N)}{12}}+\textcolor{grey}{\sum\limits_{r=2}^k\frac{(-1)^{r+1}B_{r+1}}{(r+1)!}f^{(r)}|_0^N}+I_k$
代入后消去对应彩色部分，令 $N\to+\infty$ (灰色部分趋于 $0$ )，得 $P(v)=\int_0^\infty\frac{xve^{-xv}}{1-e^{-xv}}\text dx+\log\sqrt\frac{v}{2\pi}-\frac v{24}+I_k$ .

注意 $\int\frac{xe^{-x}}{1-e^{-x}}\text dx\overset{y=1-e^{-x}}=\int \frac{-\log(1-y)}{y}\text dy=\sum\limits_{k\geq1}\frac{(1-e^{-x})^k}{k^2}$ ，故 $\int_0^\infty\frac{xve^{-xv}}{1-e^{-xv}}\text dx\overset{y=vx}=\frac{1}{v}\int_0^{\infty}\frac{ye^{-y}}{1-e^{-y}}\text dy=\frac{\pi^2}{6v}$ . 所以有：

$$P(v)=\frac{\pi^2}{6v}+\log\sqrt\frac{v}{2\pi}-\frac v{24}+I_k$$.