(题目中,我们用一“块”代指一个多格骨牌。)
(In this problem, each "piece" is a polyomino.)
下面是一道有意思的题目:
Here's a nice problem for y'all:
对于所有正整数 n,求最小的 k 使得你可以将一个 n × n 的区域分割成 n 块(每块大小任意),重新摆放其中 k 块,使得不存在任何方式选择剩余 n-k 中的一块继续摆放(允许旋转和翻转)?
For each n, find the minimum k in terms of n such that you can dissect a n × n square grid into n polyomino pieces (of any size), rearrange k of these pieces onto the same grid, and be left with no way to select a piece from any of the n-k other pieces and add it to the grid, allowing rotation and reflection.
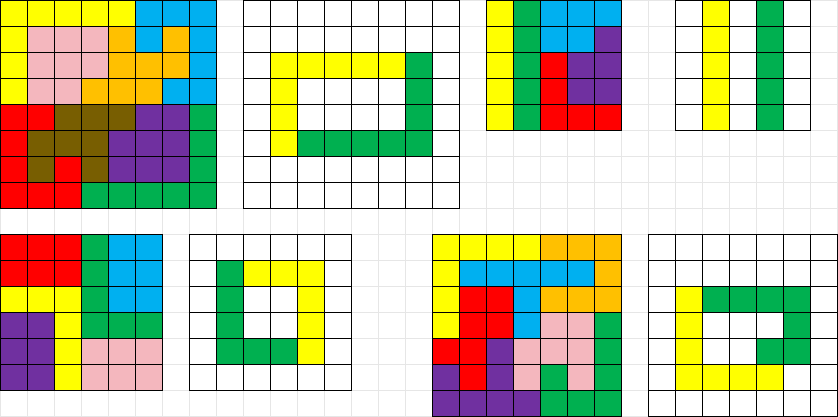
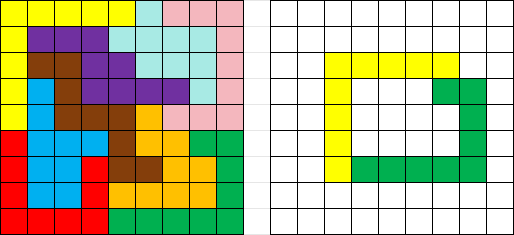
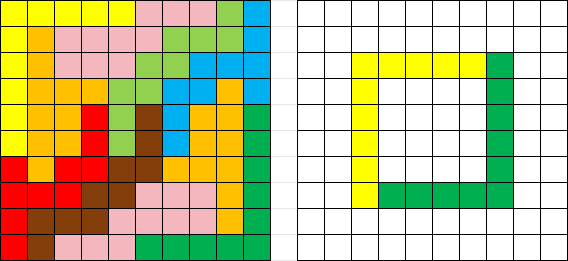
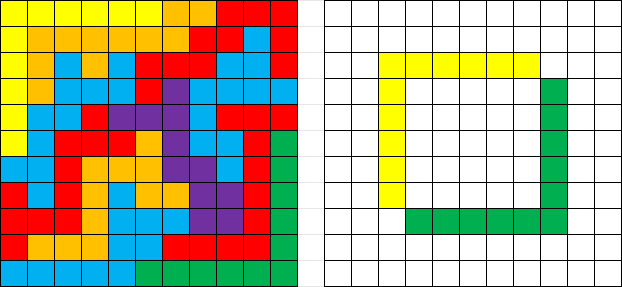
以下是 n=5,k=2 时的一个例子:
Here is an example, with n=5 and k=2:
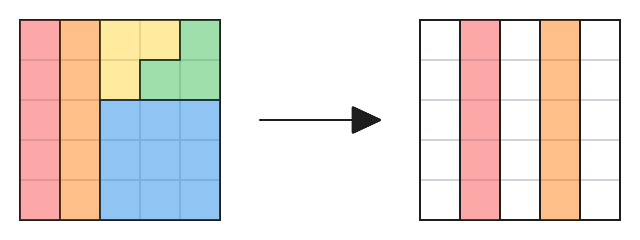
在如上图所示分割并重组其中两块之后,剩余三块中没有任何一块可以继续摆放,所以 n=5 时 k 至少可以小到 2。
After disecting our 5×5 grid as above, we can place the 2 pieces again as shown. Then, none of the other pieces can fit in, so an upper bound on the minimum k is 2.
如果要求 n 块的每一块都面积为 n 的话,结果又如何呢?
What if you restrict all polyomino pieces to n-minos?
题目出自 Omega_3301,经许可后发出。
Problem credit goes to Omega_3301, posted with permission.
希望你喜欢!
Enjoy!