对于 n*n (n≥4) 的扫雷棋盘,若最外圈(列1、n与行1、n) 上均为未翻开格,次外圈全是数字1,其余的内部方格全是翻开的空格(即数字0),记所有不同(不考虑对称去重)的雷分布情况数量为 c_n,则是否有 c_{n+3} = c_n 对于 n≥4 恒成立?
(严谨一点的表述如下图)

用 Python 穷举了 n=4~11,都是符合规律的,但是不太会证
对于 n*n (n≥4) 的扫雷棋盘,若最外圈(列1、n与行1、n) 上均为未翻开格,次外圈全是数字1,其余的内部方格全是翻开的空格(即数字0),记所有不同(不考虑对称去重)的雷分布情况数量为 c_n,则是否有 c_{n+3} = c_n 对于 n≥4 恒成立?
(严谨一点的表述如下图)

用 Python 穷举了 n=4~11,都是符合规律的,但是不太会证
条件等价于:$R_n$ 矩阵形如 且从外到内第1层的 $0$ 为中心的九宫格恰有一个 $1$
且从外到内第1层的 $0$ 为中心的九宫格恰有一个 $1$
(1) 是;
(2) 若(1,1)为1,则为 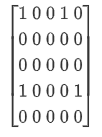 但 $b_{4,3}=0$ 矛盾。故四个角均为0。除了(1)问中的构造及其对称外,其他的必在3行或3列有1,不妨在(1,3),从而第一行为 (0 0 1 0 0),导致2 3 行全0,而4行首尾为1,进而导致第五行全0,矛盾。故 $c_5=2$.
但 $b_{4,3}=0$ 矛盾。故四个角均为0。除了(1)问中的构造及其对称外,其他的必在3行或3列有1,不妨在(1,3),从而第一行为 (0 0 1 0 0),导致2 3 行全0,而4行首尾为1,进而导致第五行全0,矛盾。故 $c_5=2$.
(3)是。第一行去掉首尾两项后以3为周期,第一列、最后一行、最后一列类似,故从可以将 n+3 与 n一一对应。