具体问题如下图所示:
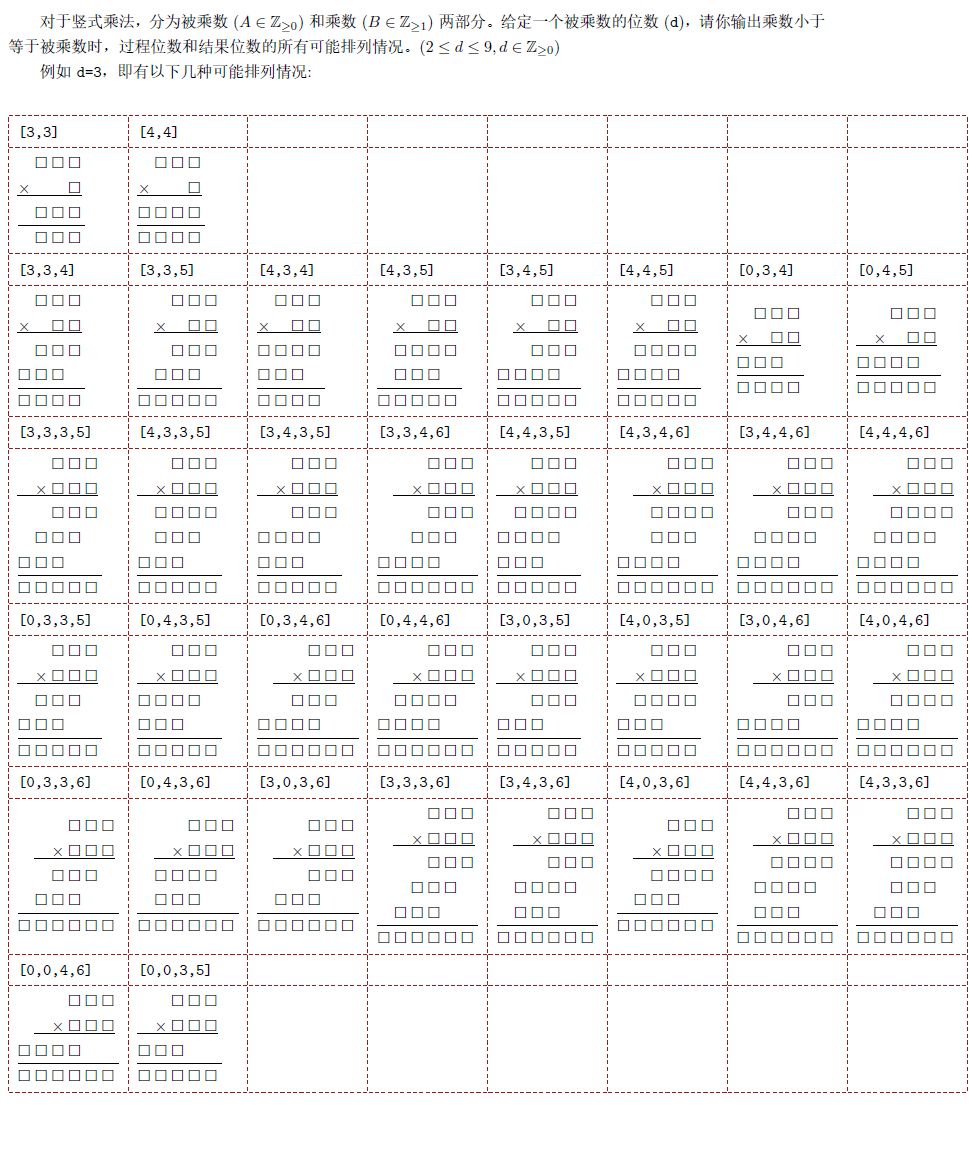

如果困难,可以告诉我 d 对应的可能排列情况总数,目前来说 d=1,2,3,4 对应的是 n=1,10,36,116 我猜测 $n=\frac{1}{2}(3^{d+1}-2d-3)$.
具体问题如下图所示:


如果困难,可以告诉我 d 对应的可能排列情况总数,目前来说 d=1,2,3,4 对应的是 n=1,10,36,116 我猜测 $n=\frac{1}{2}(3^{d+1}-2d-3)$.
难道不是算出总数比枚举所有情况更困难吗 ()
先枚举乘数的位数 $k=1,\cdots,d$。注意到中间过程的每个数是独立的,且只有 $0,d,d+1$ 三种情况,因此可以枚举,共 $3^k-1$ 种情况。枚举的复杂度是 $\sum_{k=1}^d(3^k-1)=O(3^d)$。
算最后结果的位数时,直接算可能的最小和最大位数,用极端情况贪心地给被乘数、乘数的每一位、或者过程的每一个结果赋值,然后模拟竖式运算的过程即可。
总复杂度 $O(d\cdot3^d)$。