我想知道这个积分$\int_{0}^1 x^2 \mathrm{d}x$怎么求？

$\int_0^1x^2 =\left( \frac{1}{3}x^3 \right)_0^1 = \frac{1}{3}$.

由积分公式知它等于$1/3$

这是个简单的定积分，所以直接用微积分基本定理(Newton-Leibniz)，你看一下书就知道了
也就是$$\int_{a}^{x}f(t)dt=F(x)-F(a)$$
这个F(x)就是原函数，在不定积分那章
于是$$(\frac{x^{3}}{3})_{0}^{1}=\frac{1^3}{3}-\frac{0}{3}=\frac{1}{3}$$

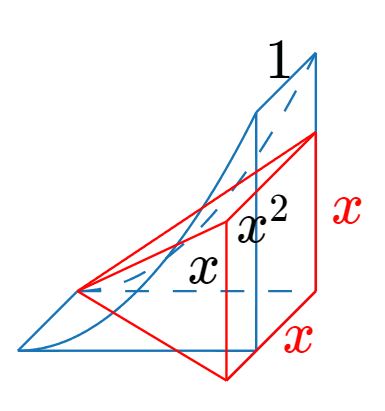
如图，底面为抛物线与x轴及垂直于x轴的线段围成的曲线三角形（两直角边长分别为$x,x^2$，面积为S），高为1的柱体（体积为V1）；底面为正方形（边长为x，面积为$x^2$），高为x的三棱锥（体积为V2）。

$V1=S\times 1=S$

$V2=(x^3)/3$

由图可知，在任意x处截面积为$x^2\times 1=x^2=x\times x$

由祖暅定理，在任意x处垂直于x轴的平面所截两几何体的截面积相等，则两几何体体积相等。

V1=V2

$S=(x^3)/3$